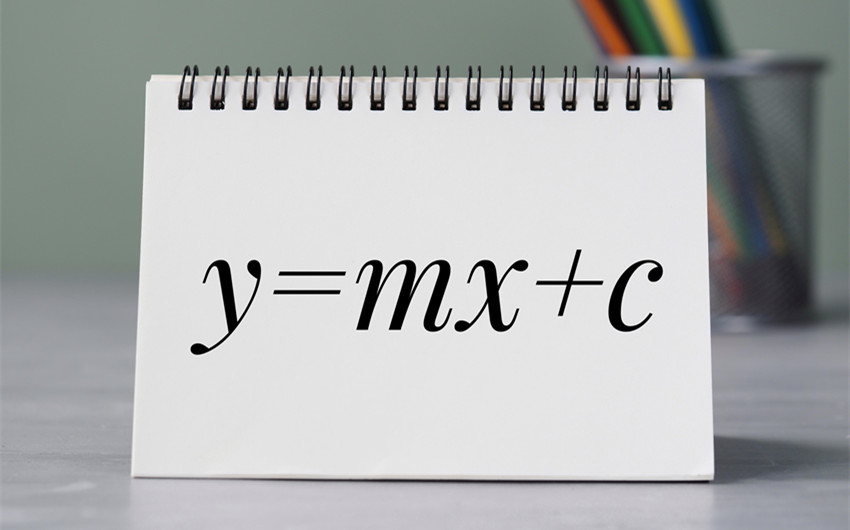What Makes a Non Proportional Relationship Example Simple
In everyday life and math class alike, not all relationships between numbers follow a perfect, even pattern. Sometimes, things just don’t grow or change at the same rate—and that’s where non-proportional relationships come in.
If you’ve ever wondered why some lines on a graph don’t go through the origin or why certain costs don’t scale evenly, understanding a non-proportional relationship example can help make sense of it all. This article breaks it down in a simple, clear way, using real-life and math-based examples to show exactly what makes a relationship non-proportional—and how to spot the difference.
What Is a Non-Proportional Relationship?
A non-proportional relationship is one where two values do not increase at a constant rate with each other. In other words, the ratio between the two variables is not the same every time, and the relationship doesn’t start at zero. This is different from a proportional relationship, where the change in one variable always matches the change in the other, forming a straight line through the origin (0,0) on a graph.
In a non-proportional relationship, that line may still be straight—but it doesn’t pass through the origin. This happens because there’s usually a fixed amount added or subtracted in the equation, like in y = 2x + 4. That “+4” means no matter what x is, there’s always something extra changing the outcome. So the rate isn’t consistent from the very beginning.
A key clue? If you divide y by x for different values, and the result isn’t always the same, the relationship is non-proportional. This small detail makes a big difference in math problems and real-world situations.
Real-World Non Proportional Relationship Example
One of the easiest ways to understand a non-proportional relationship is through everyday situations—like a cell phone plan. Imagine a plan where you pay a flat monthly fee of $20, plus $0.10 for every minute you talk on the phone.
At first glance, it seems like your cost goes up based on how many minutes you use—and it does. But it’s not proportional, because of that initial $20 fee. Even if you don’t use any minutes at all, you still have to pay $20. That’s your starting value, and it breaks the constant ratio needed for a proportional relationship.
Let’s look at a few examples:
| Minutes Used (x) | Total Cost (y) |
|---|---|
| 0 | $20.00 |
| 10 | $21.00 |
| 50 | $25.00 |
| 100 | $30.00 |
Now try dividing y by x (when x ≠ 0). You’ll get different answers each time:
-
21 ÷ 10 = 2.1
-
25 ÷ 50 = 0.5
-
30 ÷ 100 = 0.3
This proves the relationship is non-proportional—the cost isn’t increasing at a consistent rate per minute, because that $20 flat fee changes everything. A proportional plan would have started at $0 and increased at a steady rate (like $0.10 per minute without a base fee).
This kind of non-proportional relationship is common in real life—think about subscriptions, delivery charges, or parking fees. They usually include a flat rate plus a variable cost, which makes the relationship non-proportional by design.
Mathematical Non Proportional Relationship Example
In math, a non-proportional relationship is often represented by a linear equation that includes a constant term. One of the most common forms is:
y = mx + b
In this equation:
-
m is the rate of change (slope), and
-
b is the y-intercept—the value of y when x is 0.
Now, when b ≠ 0, the line does not pass through the origin (0,0), which makes it a non-proportional relationship.
Example: y = 3x + 5
Let’s break it down:
-
The slope (3) tells us y increases by 3 every time x increases by 1.
-
The “+5” means the line starts at y = 5, not y = 0.
Let’s look at a few values:
| x | y = 3x + 5 |
|---|---|
| 0 | 5 |
| 1 | 8 |
| 2 | 11 |
| 3 | 14 |
Now, divide y by x (for x ≠ 0):
-
8 ÷ 1 = 8
-
11 ÷ 2 = 5.5
-
14 ÷ 3 ≈ 4.67
These ratios are not constant, which means the relationship is not proportional.
Compare With a Proportional Example: y = 3x
| x | y = 3x |
|---|---|
| 0 | 0 |
| 1 | 3 |
| 2 | 6 |
| 3 | 9 |
Now divide y by x:
-
3 ÷ 1 = 3
-
6 ÷ 2 = 3
-
9 ÷ 3 = 3
These values are constant, and the line passes through the origin—so that’s a proportional relationship.
The Key Difference
The presence of a non-zero y-intercept (like the +5 in y = 3x + 5) makes the relationship non-proportional. It adds a fixed value no matter what x is, which means the relationship won’t scale evenly from zero.